Autorica: Maja Kalebić
Istraživačko učenje u pravilu slijedi shemu znanstvenog istraživanja, ali istovremeno je nadpojam problemskog i projektnog učenja. Oslanja se na konstruktivističku teoriju učenja gdje se kroz aktivan razvoj mentalne konstrukcije razvijaju i formiraju sposobnosti, trajna znanja i vještine učenika. Istraživačko učenje ima svoj definiran ciklus koji kreće s pitanjem.
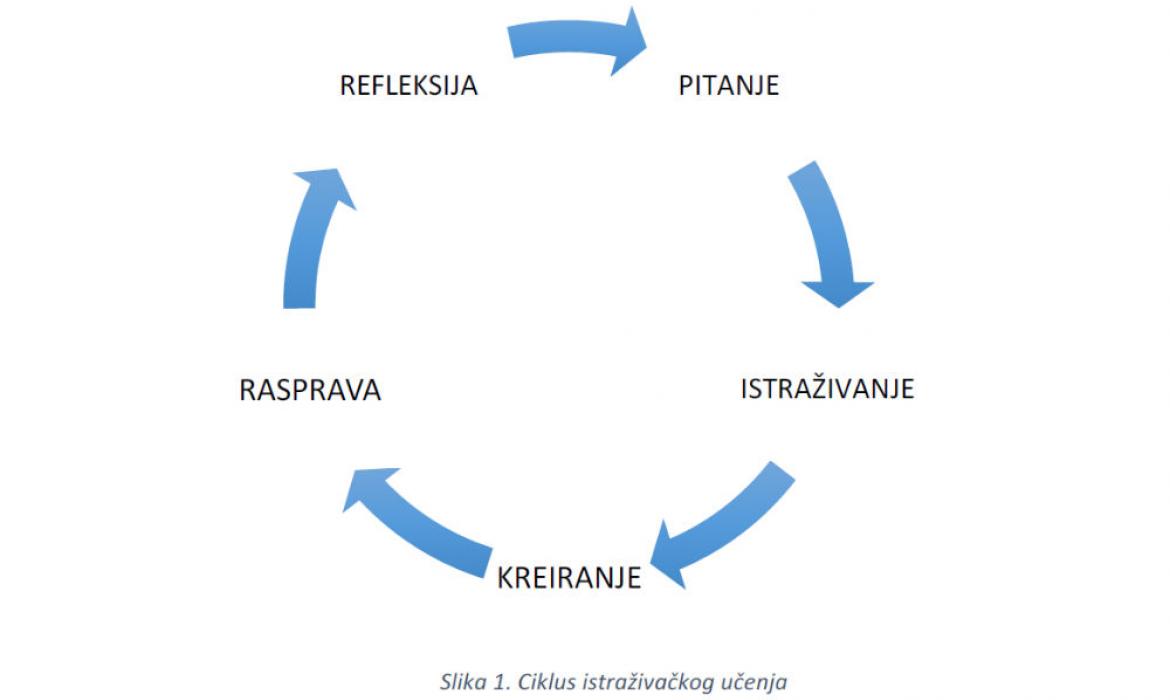
U osnovnoj školi bitno je razvijati sposobnosti kojima će se učenicima služiti u istraživačkom učenju u narednim obrazovnim fazama. Za istraživačko učenje pretpostavka su razvijeno divergentno i konvergentno mišljenje, te metakognicija kao generička sposobnost.
Divergentno mišljenje jest poseban oblik mišljenja višeg reda koje znači sposobnost generiranja raznih ideja, opcija, mogućnosti i pretpostavki. Ono otvara um prema novim idejama, te se njegovim razvojem razvija samopouzdanje učenika.
Konvergentno mišljenje predstavlja intelektualne aktivnosti koje imaju za cilj organizaciju podataka. To je mišljenje koje znači sposobnost analize i sinteze podataka i ideja tijekom traženja odgovora ili zaključaka. Konvergentno mišljenje se javlja kada učenik objašnjava, tumači, sažima i uspoređuje odnosno izvršava intelektualne aktivnosti koje imaju za cilj organizaciju podataka.
Metakognicija jest samosvijest o učenju, tj. sposobnost mišljenja o vlastitom učenju. Odnosi se na svjesno praćenje procesa učenja, postavljanja pitanja o materiji, predviđanja, aktivnosti mozga tijekom učenja. Osobito ju je bitno razvijati u osnovnoj školi kada učenik osvještava proces učenja odnosno uči kako učiti. Za kreativno mišljenje jednako je potrebno divergentno kao i konvergentno mišljenje te sposobnost metakognicije.
Projektna nastava u matematici ima velik utjecaj na razvoj kreativnog mišljenja učenika. Takav vid nastave ukazat će primjenu matematičkih znanja u stvarnom svijetu. U osnovnoj školi će u projektnoj nastavi matematike učitelj biti moderator aktivnosti indirektno postavljanjem pitanja. Pri osmišljavanju projektnog zadatka bitno je u skladu s obrazovnim ishodima koje želimo postići postaviti otvorena pitanja kao pokretače i usmjerivače cijelog procesa projektne nastave. Istovremeno, pri završavanju pojedinih faza projektne nastave, učenike je korisno naučiti koristiti zatvorena pitanja koja služe za organizaciju podataka i izvođenje zaključaka.

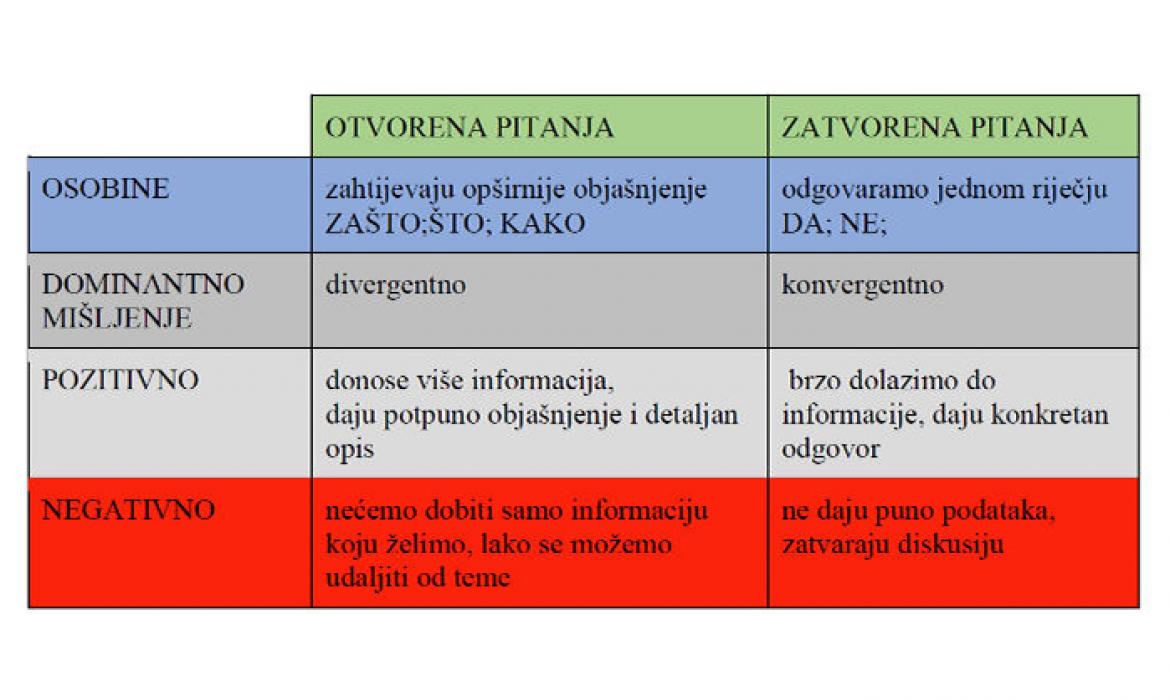
Na primjeru projektne nastave iz matematike Pravilne prizme prikazana su pitanja koja vode učenika kroz aktivnosti.









